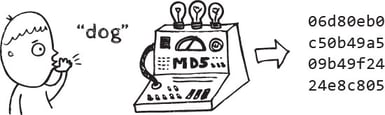
Give me any message and I will create a secret code to obscure it.
Try it!
Get the Free Pen Testing Active Directory Environments EBook
This is called hashing—a technique often used to secure passwords (among other things). Instead of keeping your secret, “dog”, in plain text for everyone to see, I’ll store the ugly 32-character code (the code is commonly called a hash).
Do I have to remember 06d80eb0c50b49a509b49f2424e8c805?
If I don’t keep the original plain-text password on file, how do I verify your password when you try to login? In other words, how does authentication happen?
It would be silly if I forced you to remember 06d80eb0c50b49a509b49f2424e8c805 every time you wanted to use your password. Instead, whenever you give me the password “dog”, I will run that text through my hash function and compare the result to the hash I have stored in my database. If it matches, you’ve authenticated successfully. Hooray!
Crucially, this only works if my hash function always generates the same output for a given input (in this case, “dog” always produces to 06d80eb0c50b49a509b49f2424e8c805). No exceptions. Cryptographic hash functions are not random.
All your hash are belong to us
The benefit of hashing is that if someone steals my hash database, they only make off with the hashes and not your actual password. Unless the hacker was able to reverse the hash values, they’re useless. Luckily for us, one of the golden rules of cryptographic hash functions is that they must be irreversible. That is, you mustn’t be able to look at 06d80eb0c50b49a509b49f2424e8c805 and figure out the input was “dog.”
In fact, the requirement is even stricter – you mustn’t be able to look at 06d80eb0c50b49a509b49f2424e8c805 and be able to find any input that would generate that same output. The fancy term for this requirement is “pre-image resistance,” which leads us to our first golden rule.
Golden Rule #1 – Pre-Image Resistance
A cryptographic hash function must be pre-image resistant—that is, given a hash function and a specific hash, it should be infeasible to find any inputs that generate that particular hash.
This is important for password security because it becomes virtually impossible for anyone to find your password (“dog”) or any other password that would hash to the same value (06d80eb0c50b49a509b49f2424e8c805) and thus give them access to your account.
The SHA-2 hash function is pre-image resistant. Don’t believe me? Here’s the SHA-2 hash of my LinkedIn password:
5c84260bcfde21e071a43fab2f6cc5c328569ea5d78aeefa156f1f1b206268b4
See you in a few millennia!
But why are hashes irreversible?
I’m going to let you in on something that is going to make this conversation even more interesting—the cryptographic hash functions that many people use—including your bank—are completely public. Anyone can get hold of the source code and see exactly how these functions work, yet the hashes are still irreversible. Why??
Think of a secure hash like grandma’s meatballs—you can’t take one of her meatballs and deconstruct it back into the exact quantities of meat, cheese, water, oil, and breadcrumbs grandma used because that information was destroyed during the cooking process. What’s more, it’s theoretically possible that multiple variations on grandma’s recipe could produce identical meatballs. So, given any one meatball, you wouldn’t be able to tell which recipe variation produced it.
Too abstract? Let’s get a little more concrete.
Pick a random number and divide it by two. Now write down the remainder. You’ve got either a 0 or 1. Now, could you take that 0 or 1 and work backwards to figure out the original number? That would be really hard to do since an infinite number of inputs—i.e., any even or odd number—could produce a 0 or 1 respectively.
Irreversibility is only the beginning
There’s a real problem with our over-simplified hash function above. It is a hash function, yes, but it’s not a cryptographic hash function. Can you see why?
While the hash produced is irreversible, it’s not pre-image resistant!
Given the hash value of 0, I can very easily produce any number of inputs that produce that hash: 2, 4, 6, 8, 10, etc. While I can’t work backwards to find your exact input, I can quite trivially find another input that maps to the same hash and, remember, when I’m authenticating I only care about comparing hashes.
Unfortunately, even when systems use cryptographically strong hash functions, there are ways for hackers to penetrate defenses. In Part 2, we’ll talk about brute-force attacks, dictionary attacks, and rainbow tables (warning: they’re not as innocent as they sound).
What you should do now
Below are three ways we can help you begin your journey to reducing data risk at your company:
- Schedule a demo session with us, where we can show you around, answer your questions, and help you see if Varonis is right for you.
- Download our free report and learn the risks associated with SaaS data exposure.
- Share this blog post with someone you know who'd enjoy reading it. Share it with them via email, LinkedIn, Reddit, or Facebook.